Suppose it's fifty years from now, and everyone considers manipulating quantum information to be routine. You're new to the quantum programming profession, still trying stuff out, and you've come up with (well, rediscovered) a clever idea for generating random data.

You call it the Hadamard coin. You'll use the fact that the X axis and Z axis of a qubit don't commute. Alternate between measuring one, then the other, and you should get results guaranteed to be random by the very laws of physics themselves!

(Uh oh, sounds like someone is rolling their own crypto...)

You try generating a list of random head/tail flips with the Hadamard coin:

def hadamard_coin_list():
    qubit = qalloc()
    result = []
    for _ in range(500):
        apply Hadamard to qubit
        if qubit:
            result.append("Heads")
        else:
            result.append("Tails")
    return result

To be a bit more concrete about how this code is supposed to work, note that each measurement of a qubit will collapse it onto the ON or OFF state. The Hadamard operation then rotates the qubit into either the state $\frac{1}{\sqrt 2}|\text{On}\rangle + \frac{1}{\sqrt 2}|\text{Off}\rangle$ or the state $\frac{1}{\sqrt 2}|\text{On}\rangle - \frac{1}{\sqrt 2}|\text{Off}\rangle$ (depending on if the qubit was ON or OFF). Measuring either of those states then gives a 50/50 random ON/OFF result, and the cycle repeats.

So far so good. You try every statistical test of randomness that you can find, and the generated lists pass with flying colors.

Later, you happen to write a method to count the number of Heads instead of putting the results into a list:

def hadamard_coin_count():
    qubit = qalloc()
    counter = 0
    for _ in range(500):
        apply Hadamard to qubit
        if qubit:
            counter += 1
    return counter

When you run this method many times and build up a histogram of counts, you expect to see a binomial distribution like this:

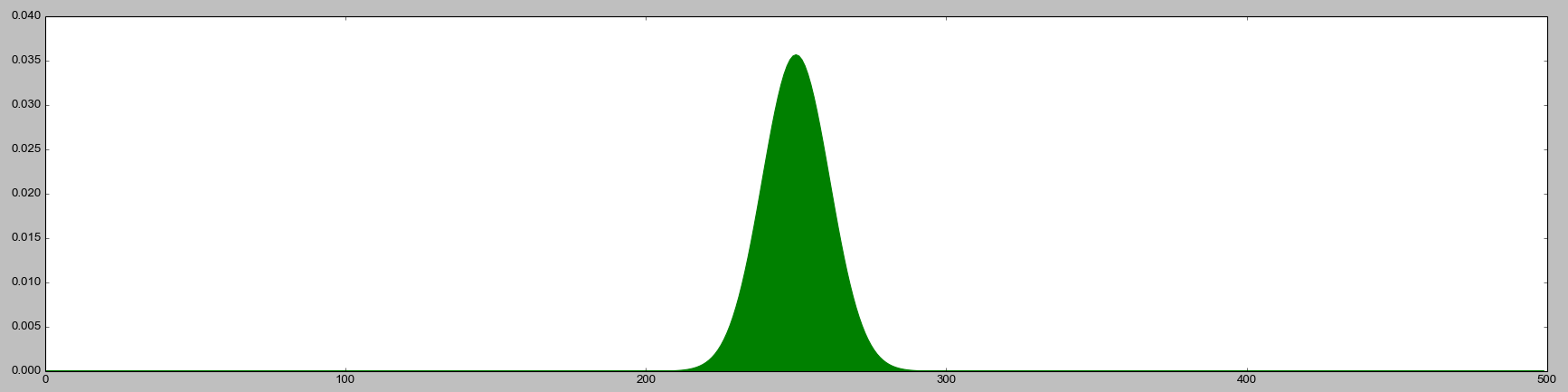
After all, the alternating measurements are producing results that follow a Bernoulli distribution. When you sum up many outcomes of a Bernoulli distribution, the total follows a binomial distribution. That's basic statistics.

So you run the method, and watch the histogram build up.

...

...

The histogram starts to take shape.

...

...

That... doesn't look quite right...

...

...

It's got... ripples?

...

...

And it's peaking towards the sides instead of towards the center!

...

...

Yeah, this doesn't look anywhere close to correct:

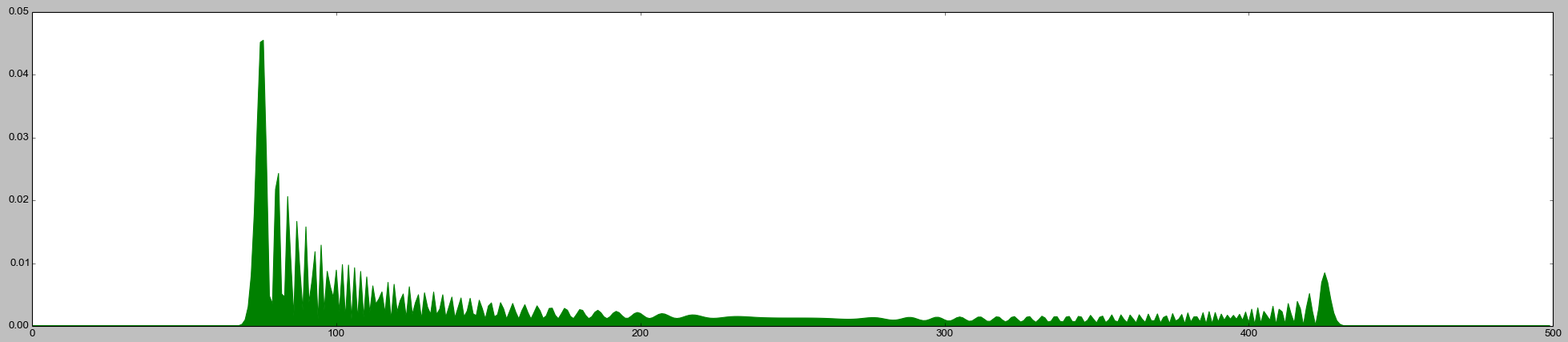
What the heck is going on? The Hadamard coin passed every statistical test you threw at it, but falls apart when counted?! Something is seriously wrong.

Implicit Measurements

The problem here is that, in quantum languages, there's an ambiguity in what it means to condition on a qubit with an if statement. There's two different "obvious" things it could mean.

Putting a qubit in the condition of an if block could mean "measure the qubit, and if the measurement result is ON then execute the following lines". That's the meaning you used when guessing that the output would look like a binomial distribution. Let's call that "de-jure measurement", because there is a rule that measurement must happen.

I think de-jure measurement is a very "classical"-ish way of thinking about if statements. In a program that handles quantum information, maintaining coherence is key. Rules that cause measurements would be a problem. Which brings us to the second possible meaning.

Putting a qubit in the condition of an if block could mean "in the generated quantum circuit, use this qubit as a control on every operation generated by this block". Whether or not this will cause a measurement depends entirely on what the operations inside the block do. Any operation that happens to cause effects that lead to outcomes that reveal the value of the condition mean that the condition was de-facto measured. But if no such operation occurs, the condition stays pure. (There are also intermediate cases that sorta-kinda-partially measure the condition.) Let's call this approach "de-facto measurement", because whether or not a measurement happens depends on what is actually done.

Your counting bug is due to expecting de-jure style measurement, but using a de-facto measurement language. When compiling the if block from the counting code, de-jure measurement outputs this circuit:

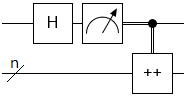
But with de-facto measurement, you get this circuit instead:

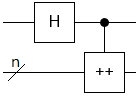
Without that measurement gate in the circuit, things get interesting. (You can see that iterating the de-facto measurement circuit 500 times matches the weird ripply distribution by simulating the circuit in Quirk. Sorry it's laggy with so many large custom operations in the toolbox. Hit 'Clear ALL' before playing around.)

When you wrote the method that stored the results in a list, the conditions were uniquely distinguished by the returned list entries. Creating and keeping the list of results caused de-facto measurement of the Hadamard coin flips.

But when you only kept track of how many flips were heads, the conditions weren't uniquely distinguished by the result. For example, there's about $10^{107}$ ways to flip a coin 500 times and get 100 heads. Since the returned total is the only distinguishing information left at the end of the method, all $10^{107}$ ways of getting 100 heads end up interfering with each other. And the reason that the graph dips towards the center is that, even though there's more ways to get 250 heads than 100 heads out of 500 flips, those paths are somehow more "balanced". The negative and positive amplitude contributions cancel out more closely, and the destructive interference overpowers the path count advantage.

In other words, forgetting to measure turned your classical random walk into a quantum random walk. So the code didn't do what you wanted... but it did vividly demonstrate that quantum random walks spread out faster than classical random walks! (It also demonstrated why de-facto measurement can be useful: it makes quantum random walks easy to write.)

Lessons

Given reasonable hypothetical quantum language features, forgetting to measure is a serious mistake that's easy to make.

Imagine if you hadn't spotted the fact that your RNG had a lack-of-measurement bug, and you plugged it into the middle of a quantum program with hundreds of thousands of lines. The symptoms would only show up under special conditions, in the statistical distribution of measurements that happen billions of instructions later... You might never even notice that something is seriously wrong.

The fact that this mistake is so easy to make, and so tricky to catch, reminds me of buffer overflows. It's worrying. Debugging big quantum programs is going to be hard.

Appendix

Code I used to generate the quantum random walk distribution plot:

import numpy as np
import matplotlib.pyplot as plt

n = 500
amps = [1] + [0]*(2*n-1)

def hadamard():
    for i in range(n):
        a, b = amps[i], amps[i+n]
        amps[i], amps[i+n] = a+b, a-b

def probs():
    p = [amps[i]**2 + amps[i+n]**2 for i in range(n)]
    t = sum(p)
    # Up until now everything has been using big-int arithmetic.
    # We need to cut them down to reasonable sizes before converting to floats.
    return np.array([float(e * 10**10 / t) / 10**10 for e in p])

def inc():
    t = amps[2*n-1]
    for i in range(n-1)[::-1]: amps[i+n+1] = amps[i+n]
    amps[n] = t

for _ in range(n):
    hadamard()
    inc()

data = probs()
plt.fill_between(
    np.array(range(n)),
    data,
    where=data>=np.zeros(n),
    interpolate=True,
    color='green')
plt.show()

Changing a-b to a+b, and dropping the **2's in the probs function, will give you a binomial distribution instead.