One of the annoying things about quantum computing is that it's not very amenable to visualization. We do have a great way to draw the state of one qubit, i.e. the Bloch sphere, but it doesn't work very well for more qubits. This makes the Bloch sphere a double-edged sword: it provides a useful tool for thinking about a single qubit, but then hinders understanding of multiple qubits. It creates confusions leading to questions analogous to "but the electron's spin has to point in some specific direction when it's entangled, right?".
Entanglement always involves two or more qubits, and the Bloch sphere is correspondingly terrible at representing entanglement. For example, looking at the Bloch sphere representation of two qubits throughout a Bell test is not very informative. All the interesting stuff is happening in the relationship between the two qubits, and the Bloch sphere fails at showing the relevant details of that relationship.
I like messing around with visualizations, so I thought I would take a crack at fixing this problem of how to visualize entanglement. This post is an after-the-fact record of the ideas I tried, what worked, what didn't, and the various little insights that iterative experimentation tends to generate.
Iteration 0
Let's start with the 2-qubit visualization that was already included in my quantum circuit simulator Quirk: the density matrix.
When it comes to doing algebra, density matrices are a great tool. When it comes to visualizing... eeehhhhhh...

The left-most display is showing the density matrix for the $|00\rangle$ state. The next display is showing the $|+0\rangle$ state. The third display is showing an entangled state that's been (temporarily) decohered; it's observationally equivalent to a 50% chance of the $|00\rangle$ state plus a 50% chance of the $|11\rangle$ state. The state is recohered for the fourth display, which is showing the entangled state $\frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$. Next we have a dynamic gate that is constantly changing what it does, so we can see what the display would show for various amounts of rotation of the first qubit around the X axis. Finally, we have some more dynamic operations. This time they're controlled, and gradually disentangle and decohere (then re-entangle and recohere) the state so we can see what that transition looks like.
With practice you can learn to eyeball information from these density matrix displays, like "if it's spread out along the main diagonal and the off-diagonal terms go away, the system is not coherent". But, in general, this is tricky to do. For example, it's hard to tell at a glance how strongly the two qubits are entangled.
We want to use concepts rooted in geometry rather than algebra. Let's try something else.
Iteration 1
When I was brainstorming ideas, one of the things I remembered is that entangled states are like unitary matrices. If you arrange the amplitudes of the $|00\rangle$, $|01\rangle$, $|10\rangle$, and $|11\rangle$ states into a 2x2 grid and pretend that grid is actually a matrix, then that matrix is (proportional to) a unitary matrix if and only if the state was maximally entangled. Separable states, on the other hand, will be equal to the matrix $\bimat{1}{0}{0}{0}$ times some unitaries. By performing a singular value decomposition, you can split any pure 2-qubit state into a combination of the separable case and the entangled case.
Why is it interesting that 2-qubit entanglement is like a 2x2 unitary matrix? Because 2x2 unitary matrices are like rotations (i.e. [SU(2)][1] is isomorphic to [SO(3)][2]). It's one of the big reasons that the Bloch sphere works so well to represent a single qubit: single-qubit operations are 2x2 unitary matrices corresponding to rotations around the Bloch sphere.
Since 2-qubit entangled states are like 2x2 unitary matrices, and 2x2 unitary matrices are like rotations... 2-qubit entangled states are like rotations! If we have a nice way to draw a rotation, then we have a nice way to draw the entangled state. (The "thing that's being rotated" is the axis $R(A)$ of qubit #1 that you learn about by measuring axis $A$ of qubit #2. For example, if two qubits are entangled such that qubit #1's X axis measurement will always agree with qubit #2's X axis measurement, then rotating qubit #1 by 90 degrees around the Z axis means that now qubit #1's Y axis measurement will always agree with qubit #2's X axis measurement. The rotation tells us how to translate between information about qubit #1 and information about qubit #2.)
A simple way to draw a rotation is to just show its effects on the X, Y, and Z axes. For each axis, apply the rotation to that axis then draw an indicator showing where the axis ended up. Additionally, we'll scale the axis indicator positions in order to show the strength of the entanglement.
The SVD we use to extract the unitary matrix corresponding to the entanglement of the system will also tell us the strength of the separable case, and the state of each individual qubit within that case. This information also characterizes the 2-qubit state, and can be represented as points on the Bloch sphere scaled by the strength of the separable case. We're already drawing the entanglement indicators on a sphere, so we might as well throw in some indicators for the separable part.
Put all that together, and you get this:

Here's pseudo-code describing the visualization in more detail:
let amps_matrix = Matrix.square(amp00, amp01,
amp10, amp11);
let {U, S, V} = amps_matrix.singularValueDecomposition();
let [s0, s1] = [S.cell(0, 0).real, S.cell(1, 1).real];
let weight_separable = s0*s0 - s1*s1;
let separable_state_1 = Matrix.row(U.cell(0, 0), U.cell(0, 1)).adjoint();
let separable_state_2 = Matrix.row(V.cell(0, 0), V.cell(1, 0)).adjoint();
let weight_entangled = 2*s1*s1;
let entangled_state_as_unitary_matrix = U.times(V);
let entangled_state_as_rotation = U2_to_SO3(U.times(V));
draw_indicator(vec_to_bloch(separable_state_1) * weight_separable, 'white')
draw_indicator(vec_to_bloch(separable_state_2) * weight_separable, 'black')
draw_indicator(entangled_state_as_rotation.rotate(point(1, 0, 0)) * weight_entangled, 'red')
draw_indicator(entangled_state_as_rotation.rotate(point(0, 1, 0)) * weight_entangled, 'blue')
draw_indicator(entangled_state_as_rotation.rotate(point(0, 0, 1)) * weight_entangled, 'green')
I think it's fair to say that this visualization is not very good.
First of all, the separable-state indicators are really distracting. The two types of indicators aren't moving in similar ways. Putting both types in one display interferes with understanding, instead of reinforcing understanding. When I try to focus on the rotation/entanglement-case indicators, my eyes keep being drawn away by the separable-case indicators swooping by.
Second, I have a hard time telling which indicator is which. The color coding isn't enough to keep them straight in my head. If the author can't keep these things straight, a user definitely won't be able to keep them straight.
Third, given how I defined this display, it only works on pure 2-qubit states. I assumed that the input was a 1x4 vector with an entry for the 00, 01, 10, and 11 amplitudes. But in practice the two qubits might be entangled with other qubits, or decohered due to a measurement, so the input will be a 4x4 density matrix. The definition needs to be generalized to work on mixed states.
I did learn something from experimenting with this display, at least. Rotating the first qubit rotates the representation in world space (i.e. relative to the X/Y/Z axes of the fixed surrounding sphere) whereas rotating the second qubit rotates the representation in model space (i.e. relative to the current X/Y/Z indicators). That's an interesting way to think about why operations on one qubit commute with operations on the other, when they're entangled.
Iteration 2
For my second attempt at representing two-qubit states, I tried to address the three problems with the first idea.
First, I dropped the separable-state indicators. They were totally redundant with the Bloch sphere representation of the individual qubits anyways. If you want to see the individual qubit Bloch vectors, Quirk already has a Bloch sphere display for that.
Second, I did a bit of polishing on the visuals. I made the axis-indicating circles larger, and gave them X/Y/Z labels. I also made them gradually scale down to nothing as they approached the origin.
Third, I generalized the math to work on mixed states. I performed an eigendecomposition of the density matrix defining the two-qubit state, which gave me a weighted combination of possible pure states. Then I separately considered the rotation defined by each case, and where that rotation would place the X/Y/Z axes. Then I literally just averaged each axis' output position across the cases, but weighted by how likely that case was.
The reasoning behind averaging the axis positions is that, if the various cases agree on where the X axis should end up, then great we should draw the axis there. And if the cases completely disagree about where the Y axis should end up, then the Y axis indicator will get pulled towards the center. This should give a nice way to distinguish between separable qubits, correlated qubits, and entangled qubits. If the qubits are separable then all the axis indicators should end up at the center, if they're entangled then all the axes should be away from the center, and if they're correlated then some axes should be pulled towards the center while others aren't.
Here's what this ended up looking like:

And here's some pseudocode describing the thing in more detail:
let vx = Matrix.col(0, 0, 0);
let vy = Matrix.col(0, 0, 0);
let vz = Matrix.col(0, 0, 0);
for (let eigen of eigenDecompose(density)) {
let M = Matrix.square(eigen.vec[0], eigen.vec[1],
eigen.vec[2], eigen.vec[3]);
let {U, S, V} = M.singularValueDecomposition();
let s = S.cell(1, 1).real;
let weight = 2*s*s;
let E = U.times(V);
let state_to_contribution = (...vec_raw) => {
let vec = Matrix.col(...vec_raw);
vec /= Math.sqrt(vec.norm2());
vec = E * vec;
vec *= vec.adjoint();
return qubitDensityMatrixToBlochVector(vec) * weight * eigen.val;
};
vx += state_to_contribution(1, 1);
vy += state_to_contribution(1, i);
vz += state_to_contribution(1, 0);
}
draw_indicator(vx, 'red', 'x');
draw_indicator(vy, 'green', 'y');
draw_indicator(vz, 'blue', 'z');
I was really happy with this visualization, except for two major flaws.
First, there's a numerical instability. See how the middle display in the above diagram has a Z indicator that's jittering up and down despite the state being constant? That's happening because there's a degeneracy in the eigendecomposition, and the specific way that degeneracy is resolved determines whether or not the Z-axis correlation is shown or hidden.
The second flaw isn't apparent in the diagram above, but was in other cases I tried. Basically, there are cases where the axes move in weird ways that hint "extra stuff" is going on. Like, there are cases where rotating one qubit will slightly pull the axes towards the center. But, given that "distance of axes from center" is supposed to be telling us how entangled the system is, that should never happen. Operations on a single qubit never change the amount of entanglement between qubits.
Because the axes appeared to be missing important information, I started wondering if sampling more directions would give a clearer result. That lead to more ideas, and eventually...
Iteration 3
Instead of pulling apart the density matrix, then applying the separated pieces to each axis, then putting the axes back together... why not just directly apply the density matrix to each axis? What if we simply consider how the possible states of one qubit informs us about the state of the other qubit? That is to say: iterate over possible states of qubit #2, project the two-qubit density matrix onto that qubit #2 state, then draw a Bloch sphere point wherever qubit #1's state ended up.
Instead of thinking about entanglement as a rotation, we've switched to thinking about entanglement as mutual information. We're asking "What are all the things that qubit A can tell me about qubit B?". The richer and more varied those things are, the more entangled the two qubits must be.
I coded up the idea, and this is what it looked like:

I also tried some other cases:
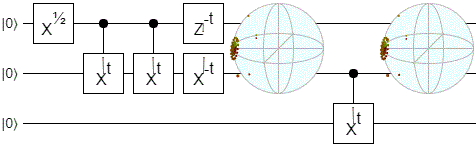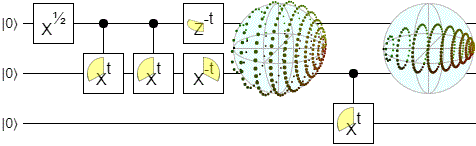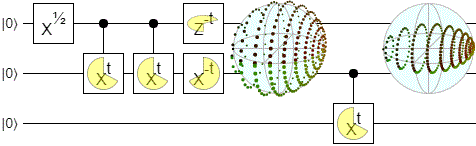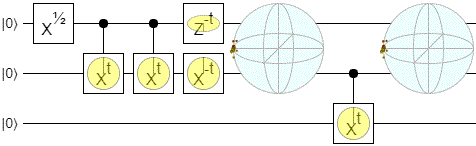
I found the above diagrams surprising. The way points slide around the outside and get drawn into the poles... in hindsight it's obvious why this happens, but I really didn't expect it ahead of time.
Did you catch what just happened? The visualization taught me something. Very good sign.
Another nice property about this display is that it has a very clear distinction between separable states, correlated states, and entangled states. Separable states look like points, correlated states look like lines, and entangled states look like balls. There's also a nice continuum between the three.
Still, there's three things I'm not too happy about with this iteration.
First, it's not symmetric. When the qubits are separable, the display is degenerating to the Bloch vector of qubit #1 and ignoring qubit #2. I'd prefer it if my two-qubit display wasn't playing favorites like that.
Second, it's not cheap to draw. I have to sample a lot of points, and the shape they make gets stretched and distorted in nonlinear ways.
Third, the points all kinda look like each other. Each point corresponds to projecting the second qubit onto some specific state, but I can't tell which point corresponds to which state. Which point is the one that corresponds to qubit #2 being in the $|0\rangle + |1\rangle$ state? I can't tell.
Iteration 4
In an attempt to make the visualization more symmetric, and to reduce the amount of distortion, I took a shot in the dark. I took the output points from the previous display, and simply scaled each by how likely its corresponding projection was to succeed. I also shifted every point over by the Bloch vector of the first qubit; I figured that would make the separable case would be drawn as a point at the center of the sphere instead of favoring one qubit over the other.
Here's what that looked like:

And pseudo-code for rescaling the points:
function second_qubit_point_given_first_trace_scaled(two_qubit_density, required_1st_qubit_amps) {
let v_pre = bloch_vector_of_2nd_qubit(two_qubit_density);
let {prob, density} = density_given_1st_qubit(two_qubit_density, required_1st_qubit_amps);
let v_post = bloch_vector_of_2nd_qubit(density);
return v_post * prob * 2 - v_pre;
}
The point cloud is no longer distorting in nonlinear ways. That's nice. But the separable states aren't doing what I expected: they're making a line across the center. I can't tell them apart from correlated states anymore.
So much for that idea, let's trying something else.
Iteration 5
One of the defining features of entanglement is that, when you learn something about one involved qubit, your best guess at the state of the other qubit moves towards the surface of the Bloch sphere. The state gets purer. The larger the increase in purity is, the more entangled the two qubits were.
So I figured, why not take Iteration 3 and scale each point by the associated increase in purity?
Here's what that looked like:

And pseudo-code:
function second_qubit_point_given_first_purity_scaled(two_qubit_density, required_1st_qubit_amps) {
let projected_density = density_given_1st_qubit(two_qubit_density, required_1st_qubit_amps).density;
let v_pre = bloch_vector_of_2nd_qubit(two_qubit_density);
let v_post = bloch_vector_of_2nd_qubit(projected_density);
let purity_pre = Math.sqrt(v_pre.norm2());
let purity_post = Math.sqrt(v_post.norm2());
let purity_increase = purity_post - purity_pre;
return v_post * purity_increase;
}
Separable states are points again; that's good. But now there's even more weird distortions of the point cloud. I have no idea what's going on with the right-most display in the above diagram as its contents approach the center.
Maybe it's time to go back to iteration 3.
Iteration 6
Iterations 4 and 5 convinced me that my attempts to make the display more symmetric were misguided. Instead of sacrificing useful visual stuff at the altar of symmetry, I decided to embrace the asymmetry.
We're iterating over possible states of qubit #2 to see how they affect qubit #1. This is very much like qubit #2 is controlling the display of qubit #1. Let's take that analogy seriously: instead of drawing a big sphere covering both wires, draw the sphere only over qubit #1 and connect it to a "for all control" on qubit #2.
I also did some more polishing of the display. In particular, I made the points corresponding to the states along the X/Y/Z axes stand out by coloring and labelling them and connecting them to the center with a line.
I think the result looks pretty good:

Separable states, correlated states, and entangled states are all easy to tell apart. When the system is fully entangled, the labelled axes act like the original rotation idea. When the system is in some weird intermediate state, the shape of the cloud gives at least some idea of what's going on. With a bit more polish, I could see actually adding this to Quirk.
Of course there are still problems. For example, because the display only covers one wire now, I had to scale down the size of the sphere. There's really not enough space for the amount of detail being drawn.
The computational cost of the display is also problematic. The dev version of Quirk I hacked this into starts to chug pretty hard if I add ten of these displays to a circuit. I would need do the computations, and maybe the drawing, on the GPU before I considered really adding this display to Quirk.
Finally, it's bad UX to introduce the concept of a "for-all" control when it only combines with the Bloch sphere display. I would want the for-all control to do useful things with other gates as well.
Update (Feb 2018): Iteration 7
In the months since writing this post, I've made a couple improvements to the display:
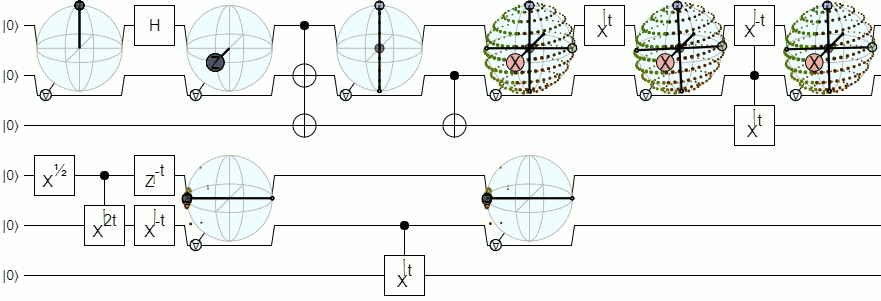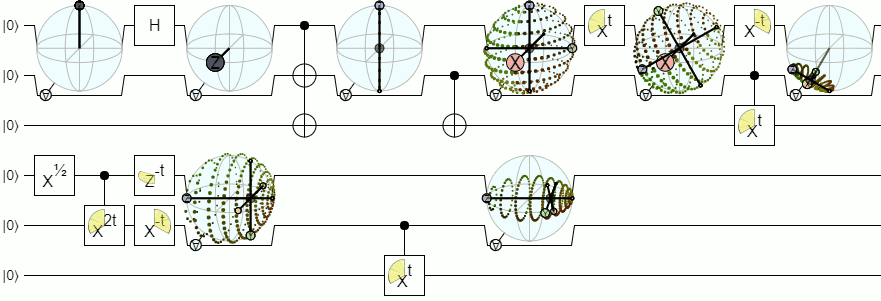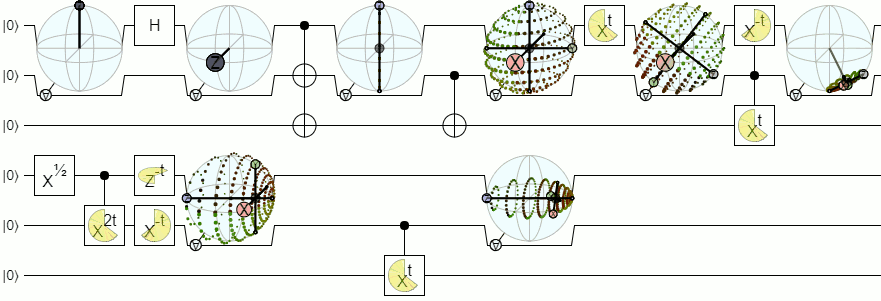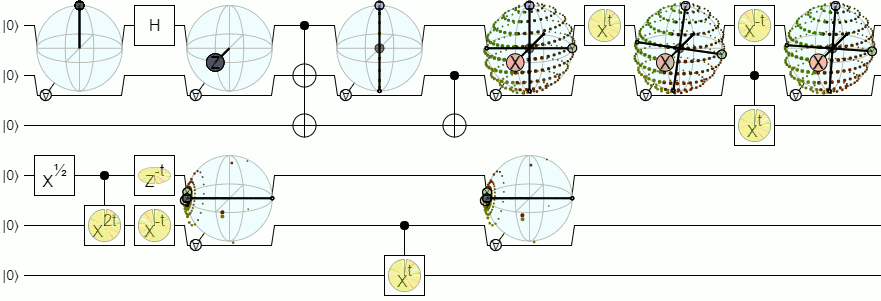
I made the display bigger by pushing the control wire down, and moving the "for-all" control to the side. I also realized it was much clearer to root the axis lines not at the origin but at the unconditioned bloch vector of the qubit. This makes the "center" of the lines move along with the shape, so that the two visually reinforce each other instead of fighting.
Closing Remarks
Pure 2-qubit entangled states are like rotations, and can be represented reasonably well as such.
Mixed 2-qubit states are harder to represent, but a point cloud corresponding to the various things one qubit can tell you about the other looks pretty cool.
I didn't find any properly symmetric ways to represent entanglement.
You can play with these displays by fetching and building the dev-entanglement-display branch from Quirk's repo.
[1]: https://en.wikipedia.org/wiki/Specialunitarygroup#n.3D2 [2]: https://en.wikipedia.org/wiki/RotationgroupSO(3)
