The delayed choice quantum eraser (DCQE) is a widely misunderstood experiment. The internet is full of questions and posts and videos and articles that seem to think the DCQE is definitive proof of time travel or some other nonsense. But, from the perspective of quantum information theory, the DCQE is very straightforward and not at all magical. So the existence of so much misguided content is pretty depressing.
It's tempting to say people are confused by the DCQE for the same reason they're confused about anything with "quantum" in the name. Quantum mechanics is known to be counter-intuitive. But I don't think "it has quantum" is the root cause of people's confusion. I think confusion over the DCQE really comes down to mistaking correlation for causation, and "quantum" just makes the mistake hard to spot.
The key property that makes the DCQE mysterious, or rather the key property that people say makes the DCQE mysterious, is the conditional appearance of an interference pattern after-the-fact. An experimenter makes a decision during an experiment, and this decision appears to determine the kind of data that was recorded earlier in the experiment. This is reasonably well summarized by a diagram from Wikipedia:
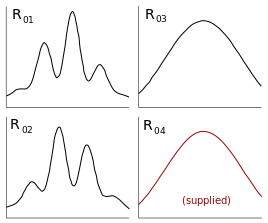
In the experiment this diagram is from, the experimenter is basically choosing whether or not to insert a beam splitter into an optical setup. The left hand column shows some measured distributions of photons landing on a screen when the beam splitter is inserted, and the right hand column shows what you get without the beam splitter.
The left hand column has wavy patterns whereas the right hand column does not, so people say stuff like "choosing to insert the beam splitter determines whether there was an interference pattern". This appears surprising, because the data being plotted in the diagrams is actually collected before anything relevant reaches the beam splitter.
Instead of explaining why this isn't as amazing as it looks in terms of the original experiment, let's remove any quantum obfuscation and do a classical experiment that has the same property. This will make it very obvious where the "magic" is coming from.
Classical delayed choice experiment
In our classical experiment, Alice will play the role of the chooser and Bob will play the role of the physical system (e.g. the photons and the screen).
Bob has a six-sided die, a two-sided coin, and a small empty box to put the coin in. He rolls the die, gets a result between 1 and 6, and places the coin in the box in a way that depends on the die roll. If the die roll was even, the coin is placed heads up. If the die roll was odd, the coin is placed tails up. Bob then writes down his die roll, and carefully hands the box to Alice.
Alice now has to decide to either a) just open the box or b) shake the box before opening it. (Shaking the box randomizes the coin.) Once the box is open, she writes down whether the coin was face up or face down, and also writes down whether or not she shook the box.
Later, after repeating the above process many times, Alice and Bob get together and compare notes. They notice something a bit confusing: Alice's choice seems to have affected Bob's results, even though Bob wrote down his results before Alice's choice!
To be specific, Alice's choice seems to determine whether or not Bob's die rolls were "banded"! Look for yourself:
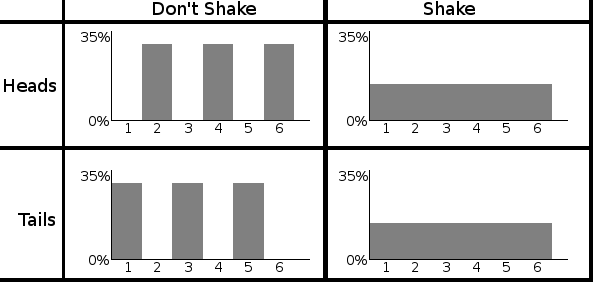
As you can see in the above diagram, Bob's die rolls depend on Alice's choice and coin results. When Alice shook the box, we see a flat distribution for Bob's die rolls. When Alice didn't shake the box, we see banded disributions.
Therefore, by the same logic people use when explaining the DCQE, Alice's choice to shake the box has reached backwards in time and changed Bob's die roll.
...
...
Just kidding. Obviously this has nothing to do with retrocausation. Alice's coin was prepared in a way that correlated it with Bob's die rolls. Of course conditioning on the coin when plotting the die rolls will show those correlations. And of course you won't see any correlation if you shake the box first. You've thrown away the correlated information by randomizing the coin!
Alice's choice wasn't whether or not to go back in time and affect Bob's die roll. Alice's choice was whether to get useful correlated information or useless random information. Trying to explain the situation in terms of Alice's choice causing Bob's die rolls to be banded is just... a weird/confused/misguided way to think about it.
Oh, and do note that Bob never directly sees a banded distribution in his die roll data. He needs to group his die rolls by the unshaken coin result in order to find anything banded. The banding is in the correlations.
Back to quantum
The quantum delayed choice experiment uses exactly the same "effect" as the classical one, i.e. it involves choosing whether or not to measure useful correlated information or else something useless.
In the same way that Alice's coin was correlated with Bob's die roll, the idler photon's state (the one that will go through a beam splitter or not) is correlated with the hit position of the screen-hitting photon. The mechanism by which this correlation is created is totally different (i.e. entanglement instead of after-the-fact preparation), but the outcome is the same.
To demonstrate the fact that the idler's state depends on the hit position, I simulated a quantum delayed choice experiment in Quirk:
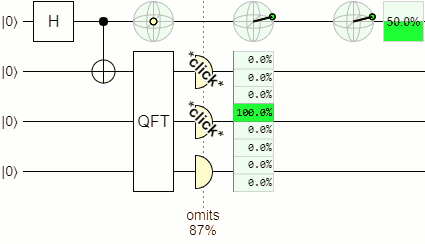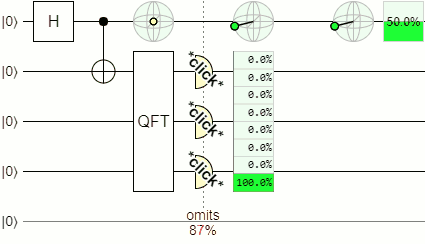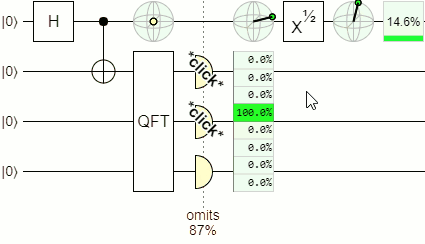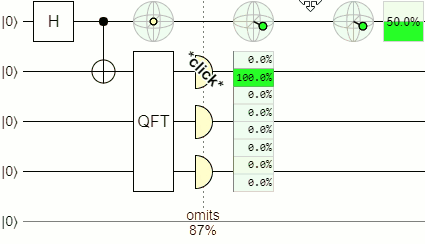
The tall green rectangle in the middle of the above diagram is showing possible screen hit positions, sampled by the click-click-clicky detectors. The green sphere above the rectangle has an indicator showing the corresponding state of the idler photon, conditioned on the displayed hit position. The further down the hit position is, the more the indicator has been rotated around the equator of the sphere.
Now comes the choice, where Alice decides whether to measure something useful or not. Again the mechanism will be different from the classical case, but the outcome will be the same.
If Alice measures the idler photon's qubit along the up-vs-down axis, the measurement is not affected by the rotation around the equator related to the hit position. The reason the measurement isn't affected is because every point on the equator is equidistance from the top and bottom, meaning the measurement is always 50/50 random. However, if Alice first rotates the qubit (by inserting that $X^{1/2}$ gate representing the beam splitter), so that the side-to-side equator rotations become top-to-bottom rotations, then the rotation around equator related to the hit position does affect the measurement probabilities.
By choosing whether or not to rotate the qubit, Alice is deciding whether or not variations from the hit position will affect her measurement probabilities. She is deciding whether to measure something useful or something useless.
When Alice picks the useful measurement, there are correlations between her result and the screen hit position. Grouping the screen hits by her result will show a wavy distribution. Grouping by the useless measurement will show a flat distribution. It's exactly like the classical case, just with quantum mechanisms. There's no time travel, no disproof of materialism, just plain 'ol correlation being mistaken for causation.
This does raise the question: is it possible to tweak the DCQE so that there isn't a classical analogue of the experiment? Well... yes. It's called a Bell test. But you'll lose all of the characteristic features of the DCQE in doing so. For example, in order to avoid the signalling loophole, the choice can no longer be delayed.
In the end, the "mysterious" parts of the delayed choice quantum eraser are just bad explanations mistaking correlations due to entanglement as causation. You'd think the fact that the "causation" was going backwards in time would have been a strong hint about that.
