Today I read the paper An Invitation to Quantum Game Theory. It's not very long, but it has a nice example of a situation where "going quantum" gives an unexpected advantage.
Quantum Q
Imagine a game between Captain Picard and Q (not sure where Alice and Bob are, but I'll stick with the characters used by the paper). The game is very simple: they will take turns either flipping or not flipping a coin without being able to see it. If the coin ends up heads, then Picard wins. Tails, Q wins.
The coin starts off tails, and the game will end after three turns. Q will get a chance to flip first, then Picard will get a chance, then Q will get to go one last time, then the coin will be revealed and the winner decided.
Classically speaking, Picard can guarantee a 50% chance of winning by randomizing his choice to flip or not flip the coin. But Q, being an omnipotent trickster, has snuck a quantum coin into the game. So Q isn't limited to just flipping the coin, he can apply any single-qubit operation he wants during his turns. Picard remains unaware and restricted to either doing nothing, or flipping the coin (flipping the coin applies an X gate to its state).
The question is: can Q use his quantum advantage to guarantee a win?
Thinking Space
Here's some space between the puzzle and my explanation of the solution.
...
...
...
You can try ideas in this or this quantum circuit simulator. Picard is only allowed to use the X gate. Q wins if the output stays in state 0.
...
...
...
...
Solution
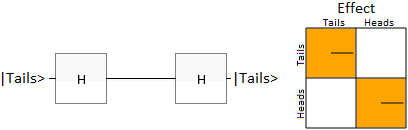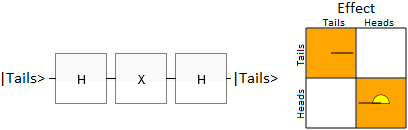
Q can win 100% of the time by applying the Hadamard operation to the coin on each of his turns. With this strategy, a coin that started off tails will end up as tails whether or not Picard flips it.
Here's an animation showing a circuit of what's going on. Picard choosing to flip the coin is represented by the presence or absence of an X gate (the quantum version of a NOT gate). But instead of flipping the coin like he expects, he ends up doing an operation that spins the phase of the "head" component of the state:
I'm guessing that, for a lot of readers, the above animation didn't convey why the solution works. Maybe something more geometric?
Geometric Explanation
A nice way to visualize the state of a qubit is the Block Sphere.
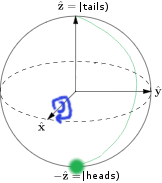
Here's a diagram, modified from the one on Wikipedia, showing the state our system starts in:

The green blob shows the starting state: at the very top, 100% tails. Other points on the surface of the sphere correspond to other quantum states the coin can be in.
Flipping the coin corresponds to rotating by 180 degrees around the X axis. From the starting state, flipping the coin would move us to the very bottom at 100% heads. Like this:
But what Q has done is first rotate the state by 180 degrees around the diagonal axis X+Z. Starting from the tails state, this rotation moves the coin's state to the front of the sphere directly along the X axis:
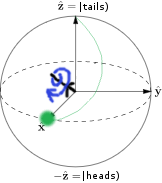
Now if Picard goes to flip the coin by rotating around the X axis, nothing will happen:
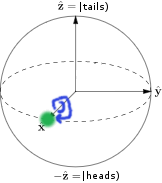
And Q can restore the tails state by rotating around the X+Z axis by another 180 degrees:
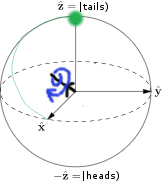
And so Q wins.
Summary
When you flip a quantum coin, you might not be doing what you think.
Part of what made this puzzle interesting to me is that I already knew $H \cdot X \cdot H = Z$, but it never occurred to me to use it as a trick. Quantum mechanics has a knack for producing surprising situations from trivial mathematical facts.
