For whatever reason, people on youtube really like to come up with weird ways to watch The Bee Movie. Case in point: "The Entire Bee Movie but every time it says bee it speeds up by 15%". (If you want a long discussion of this general phenomenon, see PBS Idea Channel's video "The Bee Movie But Every Time They Say Bee We Explain The Deal With Bee Movie".)
In this post, I want to talk about something a bit different: the fact that if you loop The Bee Movie, but keep following the 15%-faster-every-time-they-say-bee rule, you end up causing a singularity where the movie goes through an infinite number of loops in a finite amount of time.
Recursive Exponential Speedup
In the actual Bee Movie, the time from "bee" to "bee" varies. Pedagogically speaking, that's an unnecessary complication. To get a handle on how these kinds of systems behave, we'll focus on something simpler first.
Suppose we have a computer program that waits 10 "ticks", then prints the word "bee", then speeds up what a tick is by 15%, then repeats. If a tick is initially one second long, how does this program behave?
Well, at first 10 ticks is 10 seconds. So the program will sleep for 10 seconds, wake up, and print "bee". The next wait will also be for 10 ticks, but ticks will be $\frac{1}{1.15} \approx 0.87$ seconds long because of the 15% speedup. So about 8.7 seconds later, the program will wake up and print its second "bee". The third wait is 15% faster again, and takes roughly 7.56 seconds.
The 15% speedups will keep compounding: 6.58 seconds, 5.72 seconds, 4.97 seconds, 4.32 seconds, and on and on. Clearly the program will eventually end up printing "bee" at arbitrarily high rates.
To compute when the n'th "bee" should print, we can solve the power series that describes the accumulating delays:
$$\sum_{k=0}^{n-1} 10\text{s} \cdot 1.15^{-k} = 10\text{s} \cdot \frac{1 - 1.15^{-n}}{1 - 1/1.15}$$
Oh dear.
See the numerator $1 - 1.15^{-n}$? It goes up $n$ gets larger, but it's never going to be more than 1. So the time-until-$n$'th-"bee" is never going to be more than $10 \text{s} \cdot \frac{1}{1-1/1.15} \approx 76.6 \text{s}$. The million'th "bee", the trillion'th "bee", the Graham's number'th "bee"... after about a minute and a quarter, they'll all have been printed. There's a singularity.
We can see this very clearly by inverting our time-until-$n$'th-"bee" equation into a which'th-bee-at-time function $F$:
$$t = 10 \cdot \frac{1 - 1.15^{-n}}{1 - 1/1.15}$$
$$n = -\log_{1.15} \left( 1 - \frac{0.15}{11.5}t \right)$$
$$F(t) \approx -7.16 \ln(1 - 0.013 t)$$
See the problem? As $t$ increases, the natural logarithm's argument is going to go down and down until it crosses 0. This causes a singularity, at $t \approx 76.6$, where the output hits infinity:
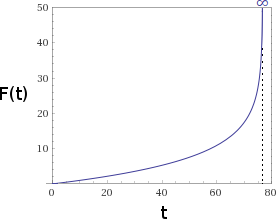
What does all of this mean? It means that our hypothetical program has to print an infinite number of "bee"s in under two minutes. Clearly we're going to need a faster computer!
Anyways, now we understand the general idea of how these make-ourselves-go-faster-including-how-often-we-get-faster systems behave. Let's apply that knowledge to The Bee Movie.
Back to the movie
If we loop The Bee Movie, and make it go 15% faster every time "bee" is spoken, it will transcend our mortal realm and graze the face of infinity. The question is: when? To answer that, we need data.
I went out onto the internet, and found a subtitles file for The Bee Movie. Here's how it starts:
2
00:00:23,869 --> 00:00:26,456
According to all known laws
of aviation,
3
00:00:26,526 --> 00:00:29,144
there is no way a bee
should be able to fly.
After suppressing the urge to roll my eyes at how wrong that line is, I grepped through the file trying to get a sense of what kinds of "bee" strings show up. Mostly there's lots of "bee" and "bees", a few "honeybee" and "beekeeper"s, and some words like "been" to avoid. All in all, there seems to be 155 instances of a "bee" word:
$ cat Bee.Movie.eng.srt | grep -owiE "(honey)?bee(keeper)?s?" | wc -l
155
Because I don't hate myself, I didn't use bash to parse the subtitles file and figure out when each "bee" word happens. I used python for that:
def bee_times_from_srt(lines):
bee_regex = re.compile('\\b(honey)?bee(keeper)?s?\\b', re.IGNORECASE)
for _, start_time, end_time, text in timed_sentences(lines):
duration = end_time - start_time
for match in re.finditer(bee_regex, text):
delay_proportion = match.start(0) / len(text) * 0.9
yield int(start_time + delay_proportion * duration)
def timed_sentences(lines):
index = 0
start = 0
end = 0
paragraph = []
for line in lines:
line = line.strip()
if not line:
yield index, start, end, ' '.join(paragraph)
paragraph = []
elif re.fullmatch('#+'.replace('#', '\\d'), line):
index = int(line)
elif re.match('##:##:##,### --> ##:##:##,###'.replace('#', '\\d'), line):
a, b = line.split(' --> ')
start = time_string_to_millis(a)
end = time_string_to_millis(b)
else:
paragraph.append(line)
def time_string_to_millis(t):
# ##:##:##,###
# 0123456789AB
hours = int(t[:2])
minutes = int(t[3:5])
seconds = int(t[6:8])
millis = int(t[9:])
return millis + 1000*(seconds + 60*(minutes + 60*hours))
Then used the python code to parse the subtitles file I downloaded:
with open(subtitles_file_path) as f:
print(list(bee_times_from_srt(f)))
# prints [27489, 34053, 36703, ..., 5163897, 5165846]
Google says the length of The Bee Movie is one hour and 35 minutes. Combine that with the times we have in hand, and we can compute how long the first run through of the movie will take:
def compute_time(speedup_times, speedup_factor, runtime):
elapsed = 0
speed = 1
at = 0
for s in speedup_times:
elapsed += (s - at) / speed
at = s
speed *= speedup_factor
elapsed += (runtime - at) / speed
return elapsed
with open(subtitles_file_path) as f:
print(compute_time(
speedup_times=bee_times_from_srt(f),
speedup_factor=1.15,
runtime=95*60*1000))
# prints 305633.40354756644
Just over 5 minutes. To be more precise: 5 minutes, 5 seconds, 633 milliseconds, and change.
Because there are 155 "bee" words in the movie, the next run will be $1.15^{155} \approx 2.56 \cdot 10^9$ times faster than the first. Which means the second loop will finish in under 3 microseconds. And the third loop will finish in less than a femtosecond.
...Yeah.
Remember how the first loop made it past 5:05.633? Infinitely many loops isn't going to make it to 5:05.634. If you sat through until the end of the first loop, you likely accidentally sat through to the end of all the loops. It's probably fine though; watching The Bee Movie infinitely many times in the span of a millisecond sounds perfectly normal and healthy.
Closing Remarks
There's an infinitely long loop of movie to get through, but we run off the end of the loop... what's going to play after that?
I'm pretty sure that the video I linked isn't compounding the speedups correctly, because I didn't transcend reality and achieve enlightenment while watching the last frame.
