This post is an addendum to Interpolating Qubit Operations and Converting Rotations into "Nice" Qubit Operations. Both of those posts are about smoothly travelling through the space of unitary operators, but they share the same massive omission (because I didn't know about it at the time).

The omission? Using the eigendecomposition to compute matrix functions like $U^t$ or $\ln(U)$ or $\exp(U)$.

Eigenvalue Functions

Unitary matrices have a lot of nice properties. A particularly nice one is that every unitary matrix can be broken into orthogonal eigenvectors. You can always break a unitary $U$ into a sum like $\sum_{\lambda,v} \lambda \ket{v}\bra{v}$, where each eigenvector $v$ is perpendicular to the others and each eigenvalue $\lambda$ is a phase factor like $e^{i \theta}$ on the complex unit circle.

Many functions on matrices ultimately amount to just transforming the eigenvalues. You want to compute an $n$'th root of $U$? Just break $U$ apart, divide the eigenvalues' phase angles by $n$, and put the matrix back together. If $U = \sum_{\theta,v} e^{i \theta} \ket{v}\bra{v}$ then the principal $\sqrt[n]{U}$ is $\sum_{\theta,v} \sqrt[n]{e^{i \theta}} \ket{v}\bra{v} = \sum_{\theta,v} e^{i \theta / n} \ket{v}\bra{v}$.

Similarly, if you want the natural logarithm of $U$ (whatever that means), then given $U = \sum_{\theta,v} e^{i \theta} \ket{v}\bra{v}$ you'll find that the logarithm is equal to $\sum_{\theta,v} \ln(e^{i \theta}) \ket{v}\bra{v} = \sum_{\theta,v} i \theta \ket{v}\bra{v}$.

Basically, when in doubt, try computing $f(U)$ by hitting $U$'s eigenvalues with $f$. It will make your life easier, and give you access to matrix functions with useful properties. Case in point, let's try using it on the two posts I linked to in the introduction.

Qubit Operations from Rotations

In the nice rotations post, I talk about mapping from rotations to operations on single qubits.

The usual way to convert from a rotation around the $\hat{v}$ axis by $\theta$ radians into a unitary single-qubit operation $U$ is to compute $U_{\hat{v}, \theta} = I \cos \frac{\theta}{2} + i \hat{v} \vec{\sigma} \sin \frac{\theta}{2}$, where $\vec{\sigma}$ is the Pauli vector, $I$ is the 2x2 identity matrix, and $i$ is $\sqrt{-1}$. The problem I had (and have) with this mapping is that it introduces an unwanted phase factor. For example, when rotating around the X axis, it won't pass through the Pauli $X$ operator. It passes through $iX$ instead of $X$. So I added a phase-correction term, did some simplification, and came up with the alternative mapping $U^*_{\hat{v}, \theta} = \frac{1}{2} I \left( 1 + e^{i \theta} \right) - \frac{1}{2} \hat{v} \vec{\sigma} \left( 1 - e^{i \theta} \right)$.

What I didn't know at the time is that both mappings correspond to exponentiation. The original mapping is just $U_{\hat{v}, \theta} = e^{i \hat{v} \vec{\sigma} \frac{\theta}{2}}$, and the phase-corrected mapping is just $U^*_{\hat{v}, \theta} = (\hat{v} \vec{\sigma})^{\theta / \pi}$. Instead of talking about "phase correction", I could have been talking about moving the $\hat{v} \vec{\sigma}$ matrix from the exponent to the base.

Moving the matrix to the base, and thinking in terms of raising it to a power, has other conceptual side effects. For example, you don't have to think in terms of angles anymore; you start to think in terms of roots. Instead of dealing with nonsense like the $\frac{\pi}{8}$ gate rotating by $\frac{\pi}{4}$ radians, you can just talk about "the [principal] $\sqrt[4]{Z}$ gate" or "the $Z^{0.25}$ gate".

Simplified Interpolation

In the interpolation post, I talk about using spherical interpolation combined with angle interpolation to smoothly move within the space of 2x2 unitary matrices.

Basically all of the machinery in that post can be replaced with this one equation: $U_s = U_0 \cdot \left( U_0^{\dagger} \cdot U_1 \right)^s$. The value $U_0^{\dagger} \cdot U_1$ is unitary, because it's a product of unitary matrices, so we can use the eigendecomposition to raise it to whatever intermediate power we want.

Despite being conceptually much simpler than the machinery from the old post, this technique also generalizes much better. It can interpolate between any two unitary matrices (of the same size), instead of just 2x2 matrices. It's even easy to write, assuming you have a linear algebra library handy. Slap together some python code to hit the eigenvalues of a matrix with a function, then use it to compute the interpolation:

import numpy

def eigenterpolate(U0, U1, s):
    """Interpolates between two matrices."""
    return U0 * eigenpow(U0.H * U1, s)

def eigenpow(M, t):
    """Raises a matrix to a power."""
    return eigenlift(lambda b: b**t, M)

def eigenlift(f, M):
    """Lifts a numeric function to apply it to a matrix."""
    w, v = numpy.linalg.eig(M)
    T = numpy.mat(numpy.zeros(M.shape, numpy.complex128))
    for i in range(len(w)):
        eigen_val = w[i]
        eigen_vec = numpy.mat(v[:, i])
        eigen_mat = numpy.dot(eigen_vec, eigen_vec.H)
        T += f(eigen_val) * eigen_mat
    return T

All we need now is some matrices I'd have considered tricky to interpolate between, and an animation of the output. Here's what happens when we interpolate between the identity operator and the increment operator:

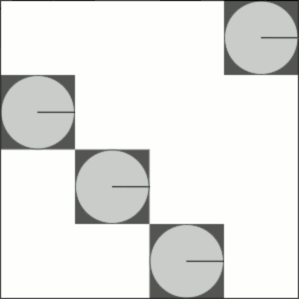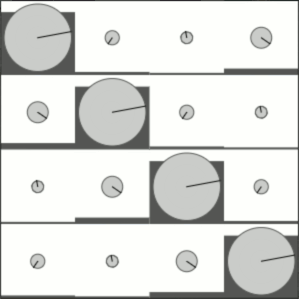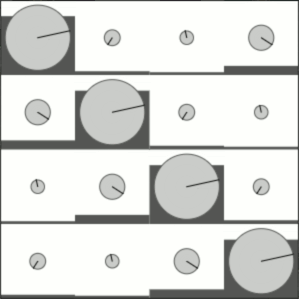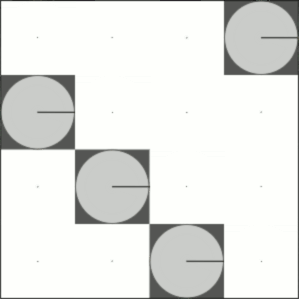
And here's interpolating between the increment operator and the fourier transform:

Finally, here's interpolating between the identity operator and the fourier transform:

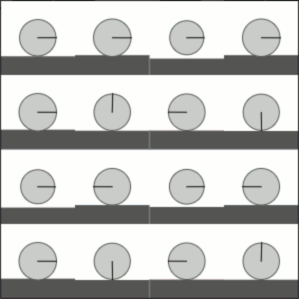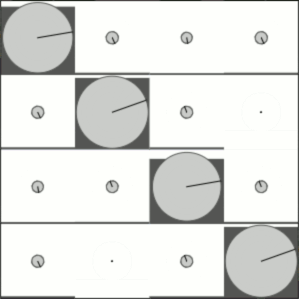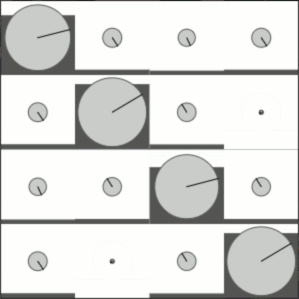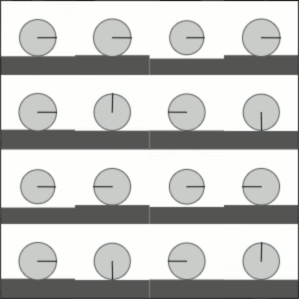
That works pretty well, for 15 lines of code! (But do 90% of them really need to include the substring "eigen"?)

(There does appear to some kind of numerical accuracy issue present. In the third animation, things don't quite line up at the pause points. I think this is numpy's fault; we're at the mercy of numpy returning good accurate eigenvectors and eigenvalues. You should have seen how bad it looked when I used $\exp(s \ln(D))$ instead of $D^s$... flickering and stuttering everywhere.)

Summary

Eigendecomposition and matrix exponentiation make everything easier. Use them.