Quantum teleportation is a technique for sending quantum information over a classical communication channel, at the cost of some pre-existing entanglement. If you're not familiar with the process, you can watch Michael Nielson, co-author of the de-facto standard textbook for quantum computing, explain it in a Khan-academy style video.
I won't be explaining quantum teleportation in detail in this post (I already did that), but for reference, here is a circuit diagram of the quantum teleportation process:
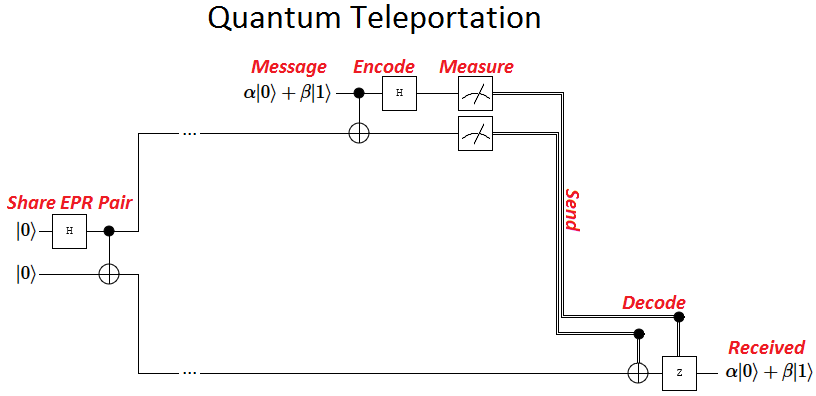
Typically, quantum teleportation is presented as a primitive. But, in this post, we will be discussing two useful sub-primitives that it can be split into. I will arbitrarily call the sub-primitives "copy-sending" and "erasure".
Copy-sending
A "copy-sending" quantum channel is one that leaves an entangled copy of the sent qubit at the sender. Specifically, a copy-sending channel performs the operation $(\alpha \ket{0} + \beta \ket{1}) \ket{0} \rightarrow \alpha \ket{00} + \beta \ket{11}$.
Note that a copy-sending channel doesn't create an independent copy, it doesn't perform the impossible task of cloning unknown quantum states, it creates entangled copies. Also note that copy-sending channels differ from typical quantum channels. Typical quantum channels move qubits (i.e. they perform $\ket{\psi} \ket{0} \rightarrow \ket{0} \ket{\psi}$) instead of copying them.
You can think of a copy-sending quantum channel as being like a long-distance controlled-NOT. The sender has the control qubit, the receiver has a target qubit in the OFF state, and the copy-send toggles the receiver's qubit when the sender's qubit is ON (without breaking superposition). But be aware of where the analogy breaks down: unlike a CNOT, copy-sending is not its own inverse. Copy-sending twice will create a second entangled copy at the receiver, instead of cancelling out the first copy.
A copy-sending quantum channel is not less powerful than a qubit-moving quantum channel, but it may be less efficient due to creating cleanup work with every coherent send.
Quantum teleportation does not act like a copy-sending channel, it acts like a qubit-moving channel. However, by cutting a few operations, we can streamline quantum teleportation into a process that performs a copy-send instead of a move. We get some benefit for our troubles: a quantum copy-teleportation only involves sending one classical bit, instead of two.
Here is a circuit diagram of the quantum copy-teleportation process (note that it's a proper subset of the quantum teleportation cicuit):
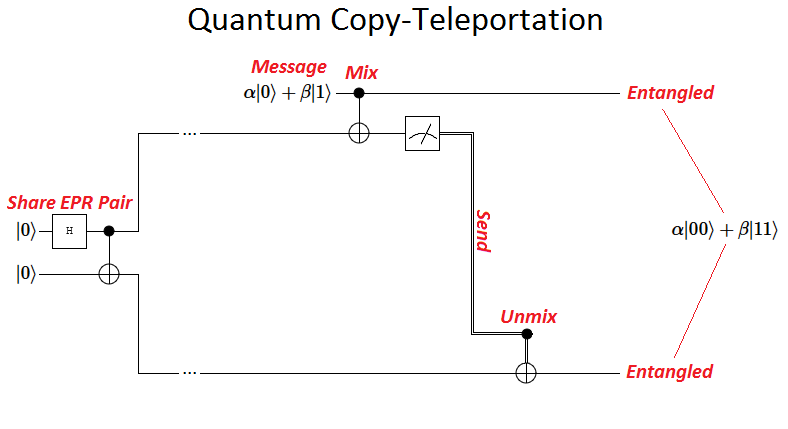
Personally, seeing the above circuit diagram for the first time gave me insight into the essence of what quantum teleportation is doing. It's using the EPR pair as a one-time pad! Alice wants to transmit a message bit $a$ to Bob, but Eve (Nature) is listening in on the line. Fortunately, Alice and Bob have a shared "really-truly" random secret bit $s$. So Alice sends $m = a \oplus s$, masking the message with the pad, and Bob receives the message by computing $m \oplus s = (a \oplus s) \oplus s = a$.
I also understand why we "use up" the EPR pair when performing teleportation now. If you re-use a one-time pad, the scheme is no longer secure because Eve would learn how various messages relate to each other. And remember that in this analogy Eve literally corresponds to Nature; she will not be fooled. (For example, it's important that Bob overwrites his copy of $s$ in computing $a$. The value $s \oplus a$ was sent classically, so any copy of $s$ will act as a de-facto entangled copy of $a$ as far as decoherence is concerned.)
So we can cut some bits off of quantum teleportation and get a copy-sending process, and this possibly gives us a few insights. But is it useful for anything? Well...
Here's a hypothetical example of a situation where copy-teleportation is useful. Suppose we have a situation with an Alice, a Bob, and a Charlie working under local operations, classical communication (LOCC) constraints. The initial state is that Bob shares an EPR pair $x$ with Alice and a separate EPR pair $y$ with Charlie. The desired final state is the threesome sharing a GHZ state (instead of the two independent EPR pairs). How do we get from the initial state to the desired state? Well, Bob can use quantum copy-teleportation, fueled by $y$, to copy-send $x$ to Charlie. This leaves Alice, Bob, and Charlie each with an entangled copy of $x$; they are in the GHZ state $\ket{xxx} = \frac{1}{\sqrt{2}}\ket{000} + \frac{1}{\sqrt{2}}\ket{111}$, as desired.
Anyways, I don't want to fret over copy-teleportation being useful or useless in practice. Let's move on to the second primitive, made up of the complementary subset of the quantum teleportation circuit.
Update (Feb 2017): Apparently, "copy-sending a qubit" is more typically called "sending a coherent classical bit". See the 2004 paper Coherent Communication of Classical Messages by Aram W. Harrow.
Erasure
I mentioned the Local Operations, Classical Communication regime in the last section. In this regime, you can perform local quantum operations but you don't have access to quantum channels (only classical ones). There are a lots of interesting tasks that you can, and can't, do under LOCC constraints (e.g. see quantum catalysis). For our purposes what matters is that you can't create entanglement under LOCC constraints... but you can erase it.
I actually covered how to do this in a previous post about kicking qubits out of GHZ states. You measure the qubit-to-be-erased along the X axis, transmit that measurement result to the receiver, and they perform a conditional phase correction. See that post for an explanation of why this works (it comes down to (1) moving Hadamard gates trades X gates for Z gates, (2) Z gates commute with their own controls, and (3) controls commute with measurements).
Here is a circuit diagram of the LOCC entanglement erasure process:
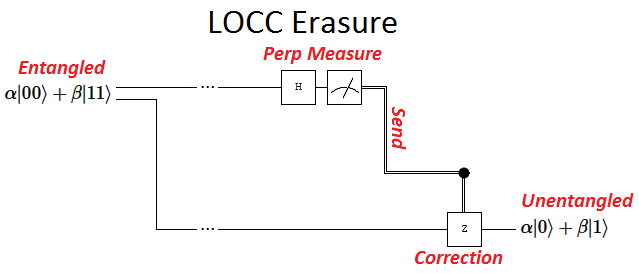
If you take the quantum copy-teleportation diagram and append the LOCC erasure diagram, you'll find that you've ended up with the full quantum teleportation diagram. That's because they are the two sub-tasks we can split quantum teleportation into, without any overlap or oversight.
Summary
Quantum teleportation can be split into two sub-tasks: a reduced form of quantum teleportation that copy-sends a qubit instead of moving a qubit, and a technique for erasing entanglement using only local quantum operations and classical communication.
Update: I should really mention that, of course, you can break down the circuit further. I picked the split I did, and stopped at that coarseness, because the result was two LOCC coordination primitives that I found interesting. Smaller pieces, like "create an EPR pair" or "perform a bell basis measurement", are also interesting (and useful!)... they just don't involve any coordination and that's where I happened to draw the line.
