(In 'Paper as Problem' posts, I treat a paper's abstract as a puzzle. "We discovered a way to X" becomes "Figure out how to do X". The goal is to solve the problem before reading the body of the paper.)

Two weeks ago, the paper "Nonlocal Measurements via Quantum Erasure" by Aharon Brodutch and Eliahu Cohen was published in Physical Review Letters. There's also a pre-print available on arXiv, which is what I read.

Based on the abstract, the paper's core contribution is:

[...] We present a scheme for effectively generating the von Neumann Hamiltonian for nonlocal observables without the need to communicate and adapt. [...]

The Problem

The paper is about measuring non-local observables involving qubits spread over multiple parties, with the caveat that the parties can't just send the qubits to each other (they don't have access to quantum channels).

For example, suppose you want to measure the Z-parity of two qubits (i.e. whether their spins agree or disagree along the Z axis). A simple way to recover the Z-parity is to measure each qubit along the Z axis, and compare the results. The problem with measuring both qubits along the Z axis, by measuring the $Z_1$ observable and the $Z_2$ observable, is that it disturbs the system more than only measuring the Z-parity observable $Z \otimes Z$.

Suppose you took two qubits and prepared them so that a bit $x$ was stored in the X-parity observable $X \otimes X$ and a bit $z$ was stored in the Z-parity observable $Z \otimes Z$ (which is the trick behind superdense coding). $X \otimes X$ commutes with $Z \otimes Z$, but it doesn't commute with $Z_1$ or $Z_2$. As a result, measuring either of the individual Z-values in the process of recovering the $z$ bit will destroy the $x$ bit. To recover both $x$ and $z$, we need to measure only the non-local observables $Z \otimes Z$ and $X \otimes X$. Not the local observables $Z_1$ or $Z_2$ or $X_1$ or $X_2$.

When both qubits are in the same quantum computer, measuring $X \otimes X$ and $Z \otimes Z$ is easy. Just CNOT one of the qubits onto the other, hit the former control with a Hadamard, then measure both qubits. But, in the paper's problem, the qubits are on separate quantum computers. We can't perform that crucial controlled-not operation.

So a concrete form of the paper's core problem is: how can measure we the Z-parity of two qubits, without disturbing the X-parity of the two qubits, when those two qubits aren't in the same quantum computer?

My Solution

After thinking for a minute, it occurred to me that quantum teleportation would make this problem trivial. If we had access to pre-shared entanglement, we could burn it to teleport Alice's qubit to Bob, have Bob perform the measurement locally, then teleport the qubit back. We'd have performed a non-local measurement, but at the cost of 2 bits of entanglement and 4 bits of classical communication to power the teleportations.

I then realized I could cut the cost in half by throwing away the second half of the first teleport and the first half of the second teleport. Copy-teleporting Alice's qubit to Bob, then erasing Bob's entangled copy after performing the measurement, is sufficient; and only costs 1 bit of entanglement and 2 bits of classical communication.

(Side note: It's tempting to think of copy-teleporting one way then erasing the other way as a sort of "temporary teleportation". That's an okay intuition for this post but, because the sender still has an entangled copy during the temporary teleport, there are caveats in the general case.)

Putting that idea into circuit form gives my guess at the solution to the paper's core problem:

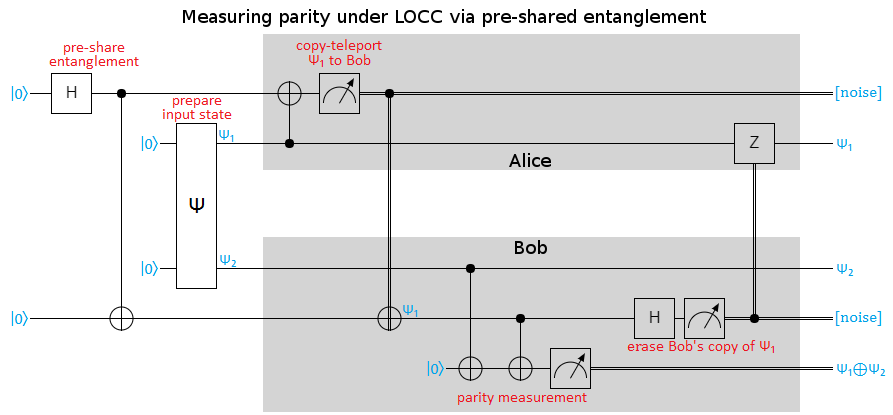
The process shown above:

• (prep) Create 1 bit of pre-shared entanglement
• (prep) Create the unknown input state $\psi$
• (prep) Give half of $\psi$ to Alice ($\psi_1$) and the other half ($\psi_2$) to Bob
• Copy-teleport an entangled copy of $\psi_1$ from Alice to Bob
  • costs 1 bit of entanglement
  • costs 1 bit of classical communication
• Perform the Z-parity measurement at Bob's, using $\psi_2$ and his entangled copy of $\psi_1$
• Erase Bob's entangled copy of $\psi_1$
  • costs 1 bit of classical communication

Note that the parity measurement can be replaced by other combined measurements of the two qubits. Also note that, although the diagram just says $\psi_1$ and $\psi_2$ for the circuit's output, the qubits storing $\psi$ have been decohered along $Z \otimes Z$ by the measurement.

After coming up with the above solution, I started worrying about the requirement of pre-shared entanglement. Was the paper going to come up with some clever way of avoiding it?

No. Definitely not.

Suppose we took two qubits, each in the unentangled state $\ket{0} + \ket{1}$, and measured their parity. If the parity measurement was even, the qubits are now in the state $\ket{00} + \ket{11}$; otherwise they're in the state $\ket{01} + \ket{10}$. By hitting one of the qubits with a NOT when the parity measurement was odd, the qubits end up unconditionally entangled into the state $\ket{00} + \ket{11}$.

In other words: a non-local parity measurement can create 1 bit of entanglement. But generating entanglement is impossible in the local-operations-and-classical-communication (LOCC) regime we're operating in (for a bunch of reasons; e.g. it would allow us to clone qubits). So it must cost at least 1 bit of entanglement to perform non-local parity measurements, else we'd be generating entanglement for free.

Performing a non-local measurement requires at least 1 bit of entanglement, and we have process that achieves that bound. Based on that, I predicted that the paper's solution to the problem was basically my circuit above.

The Paper's Solution

*Craig reads the paper.*

Argh! So close! My solution was on the right track, but I overlooked a crucial part of the problem statement: "without the need to communicate and adapt". We're not working in the regime of local-operations-with-classical-communication, we're working in the regime of local-operations-with-after-the-fact-note-comparing.

In practice, experimental physicists have a hard time bouncing messages between one quantum system and another during an experiment. It's much much easier for them to do post-processing of the results. For example, one of the recent loophole-free tests of Bell's inequality used entanglement swapping but they didn't perform the conditional phase-corrections needed to make entanglement swapping work consistently. Instead, they simply threw out the runs ruined by the lack of corrections.

That's the the easiest way to cut communication out of a protocol, after all: just post-select that it wasn't necessary. Assert that the communicated value will be 0, then compare notes after the fact and throw away any experiments that failed to meet the assertion.

The paper's solution is exactly mine, except with communication replaced by post-selection:

The entanglement and communication resources for our scheme are at most equivalent to a single round of teleportation. This can be compared to the naive strategy of teleporting, measuring and teleporting back. [...] However, the motivation for the protocol is the fact that it can be implemented without communication or adaptive components. [...] From a practical perspective we can easily imagine other situations such as linear optics, where the resources necessary for an adaptive scheme that requires communication outweigh the advantage of a deterministic protocol.

Here's the paper's diagram of their non-local measurement process:

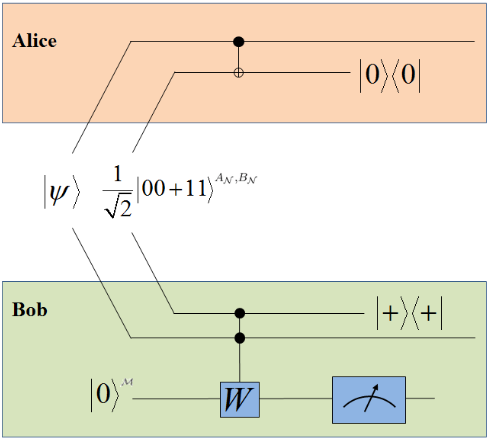
And here's the same thing again, but in my diagrammatic style (and performing a parity measurement instead of the alternative non-local measurement they were doing):

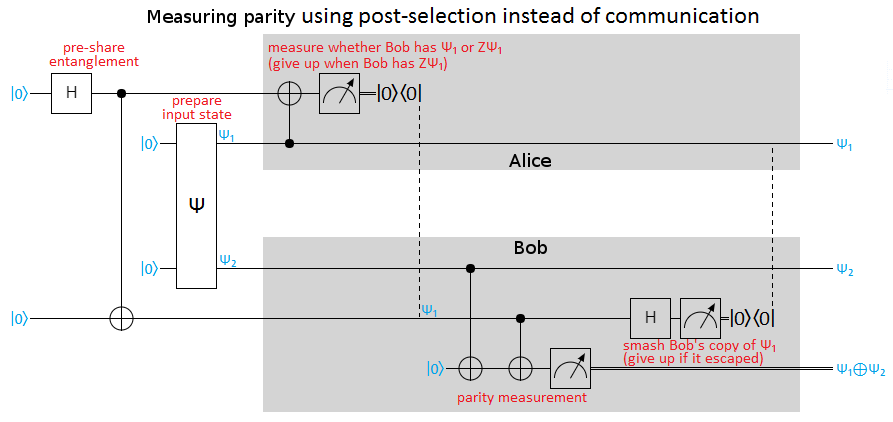
Note the similarities between the above diagram and the diagram for my initial solution. They're exactly the same, except operations controlled by remote values have been replaced with post-selection that the operation was unnecessary (due to the control not being satisfied). This avoids communication during the protocol, though of course it still requires some after-the-fact coordination where Alice and Bob tell each other which runs they ruined.

The downside of post-selecting is that we'll lose three quarters of the runs, because each post-selection has a 50/50 chance of failing. The losses get exponentially worse as the number of involved qubits increases: a non-local measurement that involves moving $m$ qubits via post-selection will only succeed $4^{-m}$'th of the time.

Summary

You can measure non-local observables by using pre-existing entanglement and post-selection to temporarily teleport entangled copies of qubits.

The paper goes into plenty of details not covered in this post, such as explaining how to parameterize the strength of the non-local measurement.

Comments