I noticed something interesting, while writing the post about implementing the QFT using addition into gradients.
Suppose you want to construct a lot of precise power-of-2 phase gates $Z^{2^{-k}}$. You're limited to Hadamard gates, controlled-NOTs, a resource state of your choosing, and the half-as-precise-as-what-you-need $Z^{2^{-k+1}}$ gate. Can you do it? For some $k$? For any $k$?
The interesting fact is this: you can succeed at this task for any $k$, except $k=2$. In this post, I discuss why that happens.
Replacing Square Roots with Controls
There's probably some fascinating underlying reason for this, but quantum circuits seem happy to let you trade affecting fewer states against applying a smaller effect to each state. Square-rooting an operation halves the strength of its effect. Controlling an operation halves the number of states it affects. But both increase the "net precision" by a factor of 2, so it's generally easy to turn one into the other (without using approximations).
Replacing a control with a square root is a standard textbook construction:
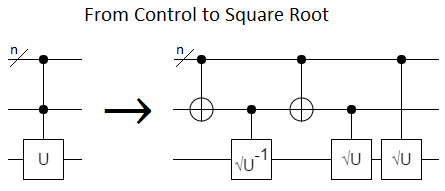
With a reusable resource state, we can also go in the opposite direction:
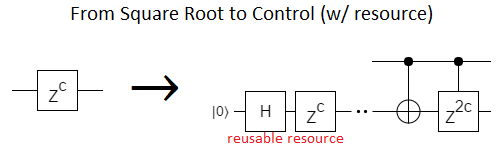
(Note: We allow ourselves any gate while making the resource, but we only get to make and use the one copy. We have to avoid messing it up when we use it, so we can re-use it again and again whenever we need the target gate. Different gates require different resources.)
If you apply the square-root-to-control construction iteratively, you create NOTs with more and more controls. The process burns itself out once you hit $Z^1$, leaving a triangle of NOTs with more and more and controls acting on a gradient resource:
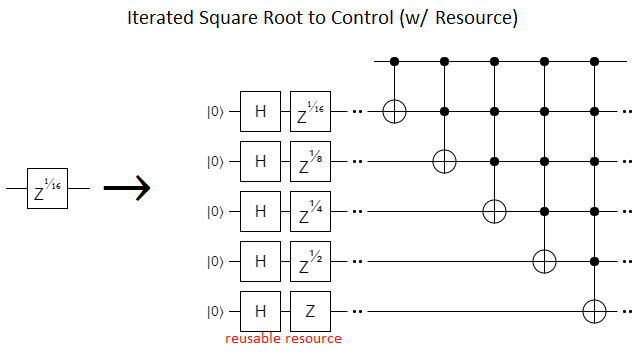
The triangle of NOTs is equivalent to a controlled decrement gate, which leads naturally into addition/subtraction, and now you know the origin story of the already-mentioned Fourier-from-addition post.
This "it turns into an increment" thing is the underlying reason we can construct $Z^{2^{-k}}$ gates out of less precise gates when $k>2$. We can turn an increment into Toffoli gates, we can turn Toffoli gates into Hadamard, Controlled-NOT, and $Z^{1/4}$ gates, and then we're done.
For $k=0$ and $k=1$ the construction is trivial, requiring only Controlled-NOT and Hadamard gates (plus the resource):
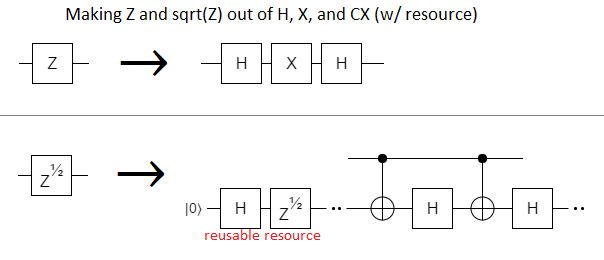
So that just leaves the $k=2$ case.
At first it seems like this case should also be easy, but you quickly realize the catch-22. This is the first $k$ where our iterated construction creates a doubly-controlled NOT, i.e. Toffoli gates:
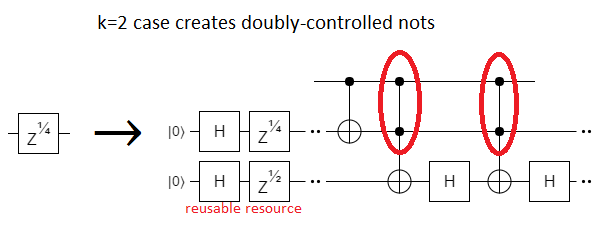
This is a problem because, to make Toffoli gates, we need more than just Hadamards, Controlled-Nots, and $Z^{1/2}$ gates. We need $Z^{1/4}$ gates to make Toffoli gates, but we need Toffoli gates to make $Z^{1/4}$ gates. We're stuck.
There are gates besides the $Z^{1/4}$ gate that would save us, of course. A particularly elegant one would be the controlled Hadamard gate:
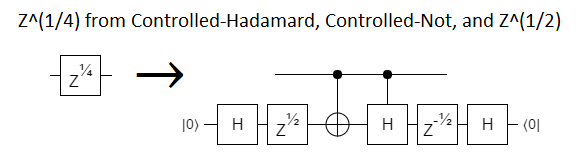
But we don't have controlled Hadamards, and we can't make them for the same reason we can't make a $Z^{1/4}$.
Stabilizer Circuits
The reason we can't make a $Z^{1/4}$ out of $X$, $H$, and $Z^{1/2}$ gates is because those three gates are Clifford gates, but $Z^{1/4}$ isn't.
The circuits you can make out of Clifford gates, called stabilizer circuits, can only implement operations from the Clifford group. Stablizer circuits are easy to simulate on a classical computer, but of course that comes with many downsides. For $n$ qubits, there are infinitely many possible stabilizer circuits... but only $\Theta(8^n)$ possible Clifford operations for them to implement. That's exponentially large, but finite.
Contrast $8^n$ with the infinity of operations we can make if we have access to the $Z^{1/4}$ gate (or any other non-Clifford gate). As soon as we have a non-Clifford gate, we can make a combination of gates that performs a rotation by an irrational fraction of a cycle. Repeating that one rotation different numbers of times gives you arbitrarily many distinct operations. Arbitrarily more than $8^n$.
There's a clear disparity in number-of-achievable-operations here, and throwing a resource state in at the start won't change anything. Regardless of what that resource is, we only have a finite number of things we can do to it. Prefixing a complicated setup step onto every operation in a finite set won't increase the cardinality of the set. Therefore we can't make a $Z^{1/4}$, since that would contradict the number of reachable operations being finite.
The only gotcha to the cardinality-based proof I just gave is measurement. Measurement is equivalent to CNOT-ing onto a fresh ancilla, but adding a fresh ancilla (even though we can't operate freely on it) is tantamount to increasing $n$ at will. So it's conceivable that there might be some clever resource state, and sequence of measurements, that gives an unbounded set of operations. After all, stabilizer circuits can at least do universal quantum computation when given a stream of resource states.
That being said... I'm just playing devil's advocate. For raw stabilizer circuits it's known that measurement doesn't add any power, and I seriously doubt that adding a resource state would help. It would just be way too convenient. The $Z^{1/4}$ gate is by far the most expensive part of quantum algorithms, to the point where you can often just ignore all the other gates when estimating costs. If there was such an easy workaround, it would already be known.
I don't know the trick to proving measurement doesn't help, but I'm sure that trick exists (and is already known). Escaping Clifford space with a single resource state? No way.
